

Next:Choice
of parametersUp:SSA
detection of structuralPrevious:Heterogeneities
in time series
Description of the algorithm
Let 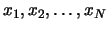 be a time series, where
be a time series, where 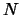 is large enough (possibly,
is large enough (possibly, 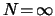 ).
Let us choose two integers: an even integer
).
Let us choose two integers: an even integer 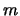
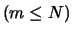 ,
the window width, and
,
the window width, and 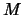
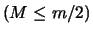 ,
the lag parameter. We also set
,
the lag parameter. We also set 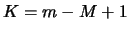 .
For each
.
For each 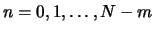 we take the time intervals
we take the time intervals![$[n+1,n+m]$](IMG67.GIF) and construct the trajectory matrices
and construct the trajectory matrices
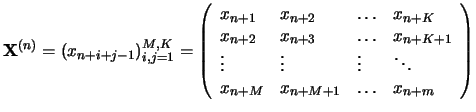
|
(4) |
The columns of 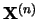 are the vectors
are the vectors 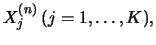 where
where
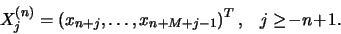
For each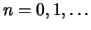 we define the lag-covariance matrix
we define the lag-covariance matrix 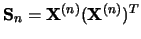 .
The SVD of
.
The SVD of 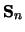 gives us a collection of
gives us a collection of 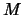 eigenvectors, and a particular combination of
eigenvectors, and a particular combination of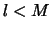 of them determines an
of them determines an 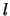 -dimensional
subspace
-dimensional
subspace 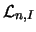 in the
in the 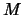 -dimensional
space of vectors
-dimensional
space of vectors 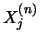 .
We denote the
.
We denote the 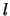 eigenvectors that determine the subspace
eigenvectors that determine the subspace 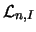 by
by 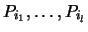 and the normalized sum of squares of the (Euclidean) distances between
the vectors
and the normalized sum of squares of the (Euclidean) distances between
the vectors 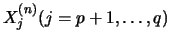 and this
and this 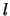 -dimensional
subspace by
-dimensional
subspace by 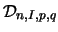 .
The normalization is made to the number of vectors
.
The normalization is made to the number of vectors 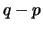 considered and the lag parameter
considered and the lag parameter 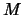 .
Since the eigenvectors are orthogonal and their norm is one, the square
of the Euclidean distance between an
.
Since the eigenvectors are orthogonal and their norm is one, the square
of the Euclidean distance between an 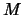 -vector
-vector 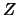 and the subspace
and the subspace 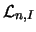 spanned by the
spanned by the 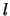 eigenvectors
eigenvectors 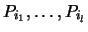 ,
is just
,
is just
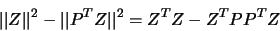
where 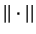 is the usual Euclidean norm and
is the usual Euclidean norm and 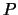 is the (
is the (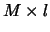 )-matrix
with columns
)-matrix
with columns 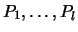 .
Therefore
.
Therefore
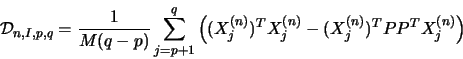 |
(5) |
For fixed  the part of the sample
the part of the sample 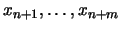 that is used to construct the trajectory matrix
that is used to construct the trajectory matrix 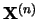 will be called the `test sample', and another subseries,
will be called the `test sample', and another subseries, 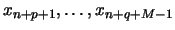 ,
which is used to construct the vectors
,
which is used to construct the vectors 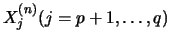 and thus to compute the normalized sum of squared distances
and thus to compute the normalized sum of squared distances 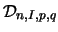 ,
will be called the `test sample'. Of course, the base and test samples
may intersect. We shall however assume that
,
will be called the `test sample'. Of course, the base and test samples
may intersect. We shall however assume that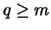 ,
so that the test sample is not strictly a subsample of the base sample.
In the most interesting case
,
so that the test sample is not strictly a subsample of the base sample.
In the most interesting case 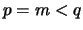 with, say,
with, say, 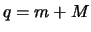 .
If a change in the mechanism generating
.
If a change in the mechanism generating 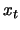 occurs at a certain point
occurs at a certain point 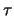 ,
then we would expect that the vectors
,
then we would expect that the vectors 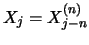 with
with 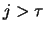 lie further away from the
lie further away from the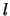 -dimensional
subspace
-dimensional
subspace 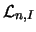 than the vectors
than the vectors 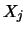 with
with 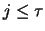 .
This means that we expect that the sequence
.
This means that we expect that the sequence 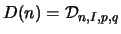 ,
considered as a function of
,
considered as a function of 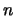 ,
starts growing somewhere around
,
starts growing somewhere around 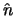 such that
such that 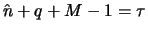 .
(This value
.
(This value 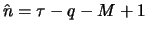 is the first value of
is the first value of 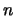 such that the test sample
such that the test sample 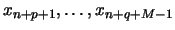 contains the point with a change.) This growth continues for some time,
the expected time of the growth depends on the signal and the relations
between
contains the point with a change.) This growth continues for some time,
the expected time of the growth depends on the signal and the relations
between 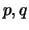 and
and 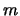 .
In the most interesting case, when
.
In the most interesting case, when 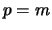 and
and 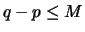 and in the case of a single change, the function
and in the case of a single change, the function 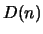 stops growing after
stops growing after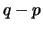 iterations, that is around the point
iterations, that is around the point 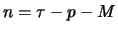 .
Then during the following
.
Then during the following 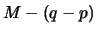 iterations one would expect reasonably high values of the function
iterations one would expect reasonably high values of the function 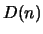 which must be followed by its decrease to, perhaps, a new level. (This
is due to the fact that the SSA decomposition should incorporate the new
signal at the intervals
which must be followed by its decrease to, perhaps, a new level. (This
is due to the fact that the SSA decomposition should incorporate the new
signal at the intervals ![$[n+1,n+m]$](IMG67.GIF) with
with 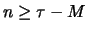 .)
Large values of
.)
Large values of 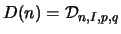 indicate on the presence of a structural change in the time series. We
also use the CUSUM-type statistics
indicate on the presence of a structural change in the time series. We
also use the CUSUM-type statistics
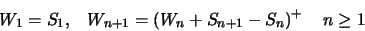
where 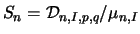 and
and 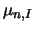 is an estimator of the normalized sum of squared distances
is an estimator of the normalized sum of squared distances 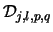 at the time intervals
at the time intervals ![$[j+1,j+m]$](IMG121.GIF) where the hypothesis of no change can be accepted. We use
where the hypothesis of no change can be accepted. We use 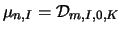 where
where 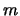 is the largest value of
is the largest value of 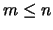 so that the hypothesis of no change is accepted. The formal description
of the algorithm is as follows. Let
so that the hypothesis of no change is accepted. The formal description
of the algorithm is as follows. Let 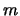 ,
, 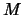 ,
, 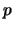 and
and 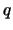 be some integers such that
be some integers such that 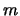 is even,
is even,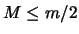 ,
, 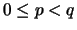 and
and 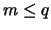 and
and 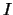 be a subset of
be a subset of 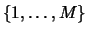 .
.
For every 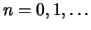 we compute:
we compute:
-
the trajectory matrix
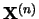 ,
see (
,
see (![[*]](cross_ref_motif.GIF) ),
),
-
the lag-covariance matrix
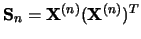 ,
,
-
the SVD of
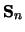 ,
and
,
and
-
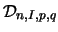 ,
see (
,
see (![[*]](cross_ref_motif.GIF) ),
the normalized sum of the squared Euclidean distances between the vectors
),
the normalized sum of the squared Euclidean distances between the vectors 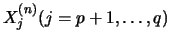 and the
and the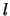 -dimensional
subspace
-dimensional
subspace 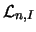 .
.
The decision rule in the algorithm is to announce the change if for a certain 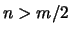 we obtain
we obtain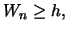 where
where 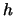 is a fixed threshold. In this case, a change in the structure of the time
series is announced to have happened at about the point
is a fixed threshold. In this case, a change in the structure of the time
series is announced to have happened at about the point 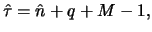 where
where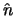 is the iteration number where the statistics
is the iteration number where the statistics 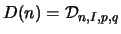 started to grow the last time before reaching the threshold.
started to grow the last time before reaching the threshold.


Next:Choice
of parametersUp:SSA
detection of structuralPrevious:Heterogeneities
in time series
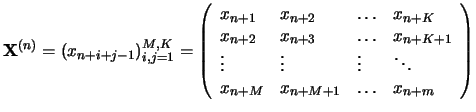
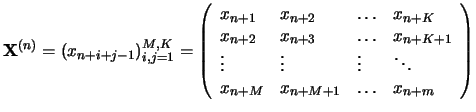
are the vectors
where
we define the lag-covariance matrix
.
The SVD of
gives us a collection of
eigenvectors, and a particular combination of
of them determines an
-dimensional
subspace
in the
-dimensional
space of vectors
.
We denote the
eigenvectors that determine the subspace
by
and the normalized sum of squares of the (Euclidean) distances between
the vectors
and this
-dimensional
subspace by
.
The normalization is made to the number of vectors
considered and the lag parameter
.
Since the eigenvectors are orthogonal and their norm is one, the square
of the Euclidean distance between an
-vector
and the subspace
spanned by the
eigenvectors
,
is just
is the usual Euclidean norm and
is the (
)-matrix
with columns
.
Therefore
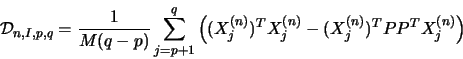
and
is an estimator of the normalized sum of squared distances
at the time intervals
where the hypothesis of no change can be accepted. We use
where
is the largest value of
so that the hypothesis of no change is accepted. The formal description
of the algorithm is as follows. Let
,
,
and
be some integers such that
is even,
,
and
and
be a subset of
.
we compute: