Heterogeneities in time series and SSA

Next: Description of the algorithm Up: SSA detection of structural Previous: SSA detection of structural

Heterogeneities in time series and SSA

The selection of a group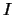

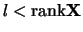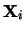of $l<{\rm rank} {\bf X}$ rank-one matrices ${\bf X}_i$ on the third step of the basic SSA algorithm implies the selection of an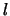

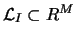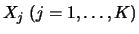-dimensional space ${\cal L}_{I} \subset R^M$ spanned by the corresponding eigenvectors of the lag-covariance matrix. One of the features of the SSA algorithm is that the distance between the vectors $X_j\; (j=1, \ldots, K)$ and the

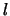-dimensional space 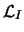${\cal L}_{I}$ is controlled by the choice of

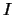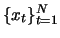and can be reduced to a rather small value. If the time series $\{ x_t\}_{t=1}^N$ is continued for

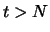and there is no change in the LRF which approximately describes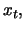

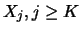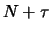then this distance should stay reasonably small for $X_j, j \geq K$ . However, if at a certain time $N+\tau$ the mechanism generating

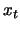
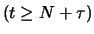$(t \geq N+\tau)$ has changed, then an increase in the distance between the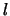

-dimensional subspace 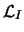${\cal L}_{I}$ and the vectors

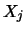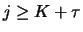for $j \geq K+\tau$ has to be expected. SSA performs the analysis of the time series structure in a nonsequential (off-line) manner. However, change-point detection problems are typically sequential (on-line) problems. In a sequential algorithm, we apply the SVD to the lag-covariance matrices computed in a sequence of time intervals

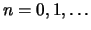. Here $n=0,1,\ldots$ is the iteration number and

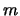is the length of the time interval where the trajectory matrix is computed. This version of the algorithm is well accommodated to the presence of slow changes in the time series structure, to outliers and to the case of multiple changes.

Next: Description of the algorithm Up: SSA detection of structural Previous: SSA detection of structural