nextupprevious
Next:SSA detection of structuralUp:SSAPrevious:SSA: choice of parameters

SSA and linear recurrent formulae

An important property of the SSA decomposition is the fact that if the original series $x_t$ satisfies a linear recurrent formula (LRF)
$\displaystyle x_t=a_1 x_{t-1}+\ldots+a_{d} x_{t-d}$ (2)

of some order $d$ with some coefficients $a_1,\ldots,a_d$, then for any $N$ and $M$ there are at most $d$ nonzero singular values in the SVD of the trajectory matrix ${\bf X}$; therefore, even if$M>d$ we only need at most $d$ matrices ${\bf X}_i$ to reconstruct the series. The fact that the series $x_t$ satisfies an LRF ([*]) is equivalent to its representability as a sum of products of exponentials, polynomials and harmonics, that is as

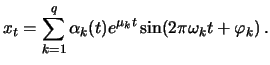$\displaystyle x_t= \sum_{k=1}^q \alpha_k(t)e^{\mu_kt}\sin(2\pi\omega_k t+\varphi_k)\, .$ (3)

Here $a_k(t)$ are polynomials in $t$, $\mu_k,\;\omega_k$ and$\varphi_k$ are arbitrary parameters. The number of linearly independent terms $q$ in ([*]) is less than or equal to $d$. We call a time series $x_1,\ldots, x_N$ ($N\leq \infty$) homogeneous if it is governed by an LRF of order $d$ that is small relative to the length of the series $N$. Of course, when we are dealing with real-life time series we can hardly hope to have a purely homogeneous time series, that is a time series governed by an LRF of small dimension (in terms of SVD, a `real-life' trajectory matrix has, as a rule, rank $M$). However, the class of series that can be approximated by the series governed by the LRFs of the form ([*]) or, equivalently, by the (deterministic) time series of the form ([*]) with a small number of terms, is very broad. We may also be interested in some periodic (perhaps, amplitude-modulated) components of the original series and in the trend, which is a residual of the time series when the noise and all oscillatory components of the series are removed. 

nextupprevious
Next:SSA detection of structuralUp:SSAPrevious:SSA: choice of parameters