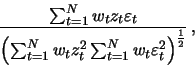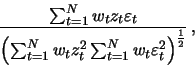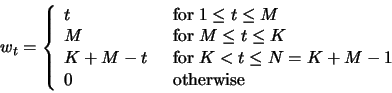

Next:SSA
and linear recurrentUp:SSAPrevious:SSA:
algorithm
SSA: choice of parameters
The parameters of the SSA decomposition are the lag parameter 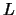 and the set of indices
and the set of indices 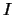 .
Their choice must depend on the properties of the original series and the
purpose of the analysis. For a properly made SSA decomposition, the component
.
Their choice must depend on the properties of the original series and the
purpose of the analysis. For a properly made SSA decomposition, the component 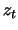 in (
in (![[*]](cross_ref_motif.GIF) )
can be identified as a trend of the original series, as an oscillatory
series (for example, seasonality) or a sum of those; the component
)
can be identified as a trend of the original series, as an oscillatory
series (for example, seasonality) or a sum of those; the component 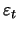 can often be associated with noise. An oscillatory series is a periodic
or quasi-periodic series which can be either pure or amplitude-modulated.
Noise is any aperiodic series. The trend of the series is, roughly speaking,
a slowly varying additive component of the series with all oscillations
removed. Note that no parametric model for the components in (
can often be associated with noise. An oscillatory series is a periodic
or quasi-periodic series which can be either pure or amplitude-modulated.
Noise is any aperiodic series. The trend of the series is, roughly speaking,
a slowly varying additive component of the series with all oscillations
removed. Note that no parametric model for the components in (![[*]](cross_ref_motif.GIF) )
is fixed and these components are produced by the series itself. Thus,
when analysing real-life series with the help of SSA one can hardly hope
to obtain
)
is fixed and these components are produced by the series itself. Thus,
when analysing real-life series with the help of SSA one can hardly hope
to obtain 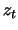 as an exact periodicity or linear trend, for example, even if this periodicity
or linear trend are indeed present in the series. This is an influence
of noise and a consequence of the non-parametric nature of the method.
In many cases, however, we can get a good approximation to these series.
In many cases some of the eigenvectors
as an exact periodicity or linear trend, for example, even if this periodicity
or linear trend are indeed present in the series. This is an influence
of noise and a consequence of the non-parametric nature of the method.
In many cases, however, we can get a good approximation to these series.
In many cases some of the eigenvectors 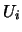 and the principal components
and the principal components 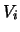 could be identified if considered as time series. The structure of those
selected for the group
could be identified if considered as time series. The structure of those
selected for the group 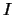 on the third step of the SSA algorithm is inherited by the series
on the third step of the SSA algorithm is inherited by the series 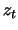 .
In the ideal situation, the components in (
.
In the ideal situation, the components in (![[*]](cross_ref_motif.GIF) )
must be `independent'. Achieving `independence' (or `separability') of
the components
)
must be `independent'. Achieving `independence' (or `separability') of
the components 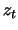 and
and 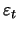 in the SSA decomposition (
in the SSA decomposition (![[*]](cross_ref_motif.GIF) )
is of prime importance in SSA. One of the characteristics of separabilty
is the so-called
)
is of prime importance in SSA. One of the characteristics of separabilty
is the so-called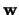 -correlation
which is defined as
-correlation
which is defined as
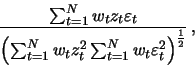
where, see Golyandina, Nekrutkin and Zhigljavsky (2001),
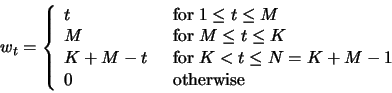


Next:SSA
and linear recurrentUp:SSAPrevious:SSA:
algorithm