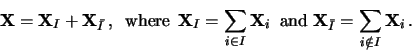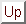

Next:SSA:
choice of parametersUp:SSAPrevious:SSA
SSA: algorithm
SSA (singular-spectrum analysis) is a novel technique of time series analysis
incorporating the elements of classical time series analysis, multivariate
statistics, multivariate geometry, dynamical systems and signal processing.
The main idea of SSA is in performing a singular value decomposition (SVD)
of the `trajectory matrix' obtained from the original time series with
subsequent reconstruction of the series. The basic version of SSA consists
of four steps, which are performed as follows (see Golyandina, Nekrutkin
and Zhigljavsky (2001) for other versions of SSA).
-
Step 1.
-
Embedding. Let
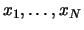 be a time series of length
be a time series of length 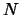 ,
and
,
and 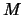 be an integer, which will be called the `lag parameter'. We set
be an integer, which will be called the `lag parameter'. We set 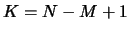 and define the
and define the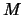 -lagged
vectors
-lagged
vectors 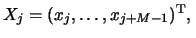
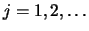 ,
and the trajectory matrix
,
and the trajectory matrix
![\begin{displaymath}{\bf X}=(x_{i+j-1})_{i,j=1}^{M,K}=[X_1:\ldots:X_{K}] \, .\end{displaymath}](IMG7.GIF)
Note that the trajectory matrix 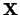 is a Hankel matrix, which means that all the elements along the diagonal
is a Hankel matrix, which means that all the elements along the diagonal 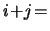 const are equal.
const are equal.
-
Step 2.
-
SVD of the trajectory matrix. Compute the singular value decomposition
(SVD) of the matrix
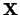 .
It can be obtained via eigenvalues and eigenvectors of the so-called lag-covariance
matrix
.
It can be obtained via eigenvalues and eigenvectors of the so-called lag-covariance
matrix 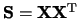 of size
of size 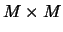 .
Denote by
.
Denote by 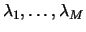 the eigenvalues of
the eigenvalues of 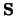 and assume that they are arranged in the decreasing order, so that
and assume that they are arranged in the decreasing order, so that 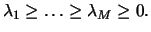 Let
Let 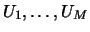 be the corresponding orthonormal eigenvectors of
be the corresponding orthonormal eigenvectors of (in SSA literature they are often called `empirical orthogonal functions'
or simply EOFs) and denote
(in SSA literature they are often called `empirical orthogonal functions'
or simply EOFs) and denote 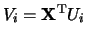 for
for 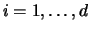 ,
where
,
where 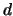 is the number of nonzero eigenvalues
is the number of nonzero eigenvalues 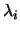 .
The vectors
.
The vectors 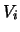 are the eigenvectors of the matrix
are the eigenvectors of the matrix 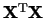 ;
they are sometimes called `principal components'. As a result of the SVD
we obtain a representation
;
they are sometimes called `principal components'. As a result of the SVD
we obtain a representation 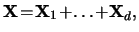 where
where 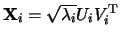
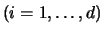 are rank-one biorthogonal matrices.
are rank-one biorthogonal matrices.
-
Step 3.
-
Grouping. Split the set of indices
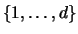 into two groups, namely
into two groups, namely 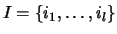 and
and 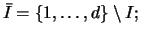 then sum the matrices
then sum the matrices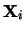 within each group. The result of the step is the representation
within each group. The result of the step is the representation
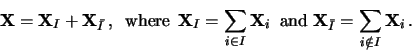
-
Step 4.
-
Reconstruction. Averaging over the diagonals
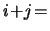 const of the matrices
const of the matrices  and
and  is performed. Applying then twice the one-to-one correspondence between
the series of length
is performed. Applying then twice the one-to-one correspondence between
the series of length 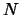 and the Hankel matrices of size
and the Hankel matrices of size 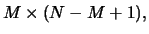 we obtain two series (denote them by
we obtain two series (denote them by 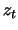 and
and 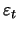 )
and the SSA decomposition, which is a decomposition of the original series
into a sum of two series
)
and the SSA decomposition, which is a decomposition of the original series
into a sum of two series
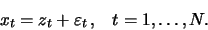
|
(1) |
Here the series 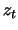 (obtained from the diagonal averaging of
(obtained from the diagonal averaging of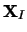 )
can often be associated with signal and the residual series
)
can often be associated with signal and the residual series 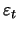 with noise.
with noise.


Next:SSA:
choice of parametersUp:SSAPrevious:SSA
is a Hankel matrix, which means that all the elements along the diagonal
const are equal.
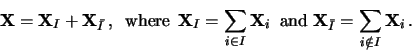
is a Hankel matrix, which means that all the elements along the diagonal
const are equal.